A series electric DC circuit is being considered to do math. The circuit contains a voltage source with its internal resistance and a load resistors. Resistance of wires is omitted in this example.
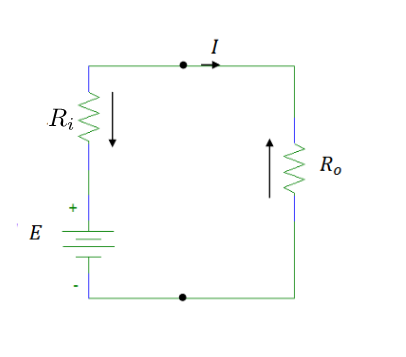
The voltage equation for the circuit above is following
E - R_i \cdot I - R_o \cdot I = 0
Thereby the current is given by the equation
I = \frac{E}{ R_i + R_o }
A general formula for power is
P = U \cdot I
Knowing that the voltage on the resistor Ro is given by the Ohm’s law relation
U(R_o)= I \cdot R_o
A formula for power on the resistor Ro is following
P(R_o)= I^2 \cdot R_o
After plugging in the relation for current
P(R_o)= (\frac{E}{ R_i + R_o })^2 \cdot R_o
The extremum of function P(Ro) needs to be found in order to find which magnitude of the resistor Ro will be give the maximum power.
The first derivative of equation of power on the resistor Ro is following
\frac{dP(R_o)}{dR_o}= \frac{d}{dR_o}((\frac{E}{ R_i + R_o })^2 \cdot R_o)
After doing the math, the theorems for derivatives of the multiplication of functions and internal and external functions were applied
\frac{dP(R_o)}{dR_o}= -2\cdot \frac{E}{ R_i + R_o } \cdot \frac{E}{ (R_i + R_o)^2 } \cdot R_o + (\frac{E}{ R_i + R_o })^2
In order to find the extremum the point where the derivative is equal to 0 needs to be calculated
0= -2\cdot \frac{E}{ R_i + R_o } \cdot \frac{E}{ (R_i + R_o)^2 } \cdot R_o + (\frac{E}{ R_i + R_o })^2
After rearranging the elements in equation above and doing some math
R_o = R_i
Finally, the maximum power on the load resistor Ro is given by formula
P(R_o)_{max} = \frac{E^2}{4 \cdot R_i}