A considered below AC electric circuit is composed of an AC voltage source, a resistor, a capacitor, an AC current source and an inductive coil. The nodal analysis method is being applied to calculate currents in the circuit’s branches. It is recalled that in the nodal analysis method it is always assumed that an electrical potential of one of nodes is equal to 0.
Since the considered electric circuit is an AC circuit following formulas are to be applied:
\underline{Z} = \frac{1}{\underline{Y}} \underline{Y} = \frac{1}{\underline{Z}}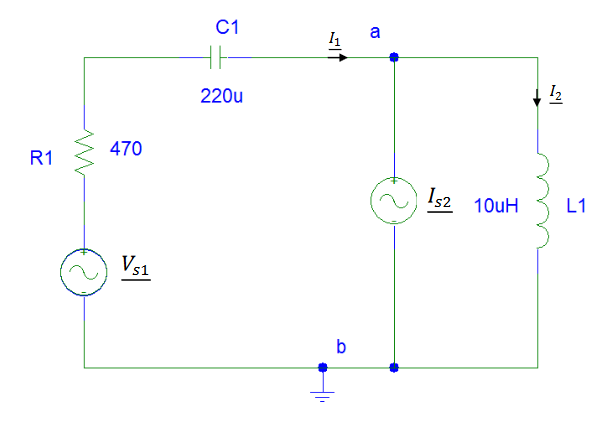
The further calculations related to the present example are available – Node voltage method example 2.