


Calculating total impedance Z in electrical AC circuits. In collection of examples you can find derivation of formulas for capacitive reactance XC and inductive reactance XL. Impedance is wider magnitude than resistance. Impedance has three components which are: resistance, capacitive reactance and inductive reactance. Impedance in general case is a vector. Components of impedance are geometric sum, because they also are vectors. Complex numbers are applied to calculate impedance and its components.
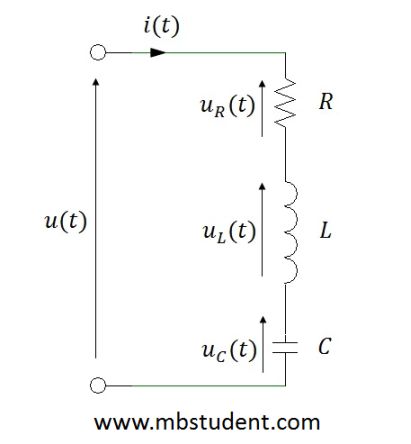
Impedance has three components. In general impedance is a vector which is built of complex number.
Z=R+j·XL-j·XC
where
• R=ρ·l/S - resistance [Ω]
• XL=ω·L - inductive reactance [Ω]
• XC=1/(ω·C) - capacitive reactance [Ω]
• ω=2·Π·f - pulsation [rad/s]
Designation of total impedance and its components for AC circuit. In example circuit impedance Z which is seen from power supply terminals will be calculated. Circuit is built from two resistors R, capacitor C and inductivity L. We will plot also vector diagram of currents and voltages in circuit.
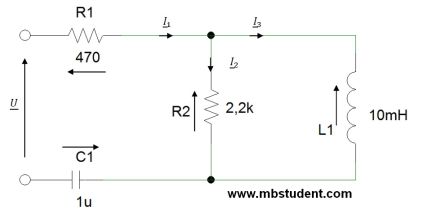
Total impedance - example 1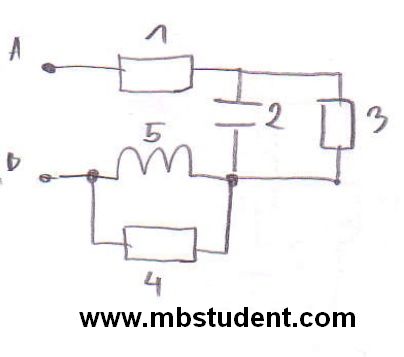
Designation of total impedance Z for electrical AC circuit. Considered electrical circuit built with three resistors R, capacitor C and inductivity L. All parts in the circuit have the same value of impedance which is 1[Ω]. Parts in circuit are connected in mixed ways because there are serial connections and parallel connections. Total impedance is designated as impedance which is seen from power terminals. In example relation between impedance Z and admittance Y will be applied → Y=1/Z.
• Z=R+j·X → Z=R+j·(XL-XC)
• Y=G+j·B

Designation of total impedance and its components for AC circuit. In example circuit impedance which is seen from power supply terminals will be calculated. Circuit is built from two resistors, two coils and one capacitor. Formulas for Ohm law in AC circuit will be also written.
Total impedance - example 3
Designation of total impedance and its components for AC circuit. In example circuit impedance which is seen from power supply terminals will be calculated. Circuit is built from three coils, three capacitors and one resistor. Ohm law in AC circuit will be also written.
Total impedance - example 4
Designation of total impedance Z and its components for AC circuit. In example circuit impedance which is seen from power supply terminals will be calculated. Circuit is built with two capacitors, inductivity and resistor. Impedances of every part in circuit is known. Circuit has mixed connections, parallel and serial . Relation between impedance Z and admittance Y will be applied → Y=1/Z.
Total impedance - example 5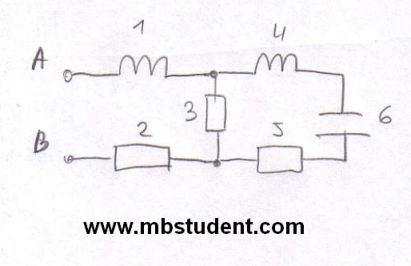
Designation of total impedance Z and its components for AC circuit. In example circuit impedance which is seen from power supply terminals will be calculated. Circuit is built with two inductivities, three resistors and capacitor. Impedances of every part in circuit is known. Circuit has mixed connections, parallel and serial . Relation between impedance Z and admittance Y will be applied → Y=1/Z. Admittance is usually used to calculate impedance of parallel connection between parts.
Total impedance - example 6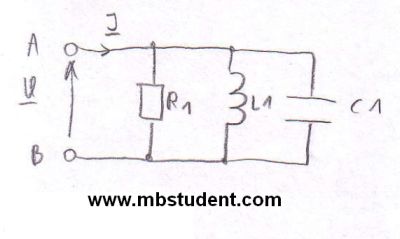
Electrical circuit is built with three passive parts, resistor R1=2[Ω], capacitor C1=2[μF] and inductivity L1=100[mH]. All parts in circuit are connected in parallel. Circuit is supplied with voltage U. Voltage's rms value is 230[VAC]. Voltage has frequency f=50[Hz]. Subject of example is calculation of current I, which flows through circuit. In example total impedance Z will be calculated. Ohm's law for AC circuits will be applied to calculate current I → I=U/Z. All calculations in example are made with application of complex numbers.
Total impedance - example 7