


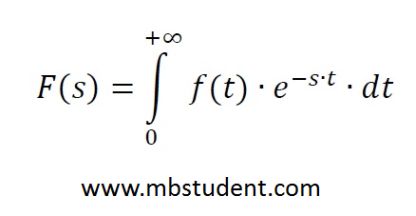
Set of examples with Laplace transformation. Laplace transformation is one of method for solving differential equations. This metod is often used in various fields of strict sciences, for example, physics, electrical engineering, and control theory. Procedure for solving differential equation with application of Laplace transformation is following:
• transform equation to Laplace form → £{f(t)}=F(s)
• write expression F(s) on equations left side, the rest on te right side
• smash left side of equation to simple fractions
• calculate factors, by which fractions are multiplied
• compare simple fractions,which are in Laplace transformation form, with formulas for basic Laplace transformation
• execute inverse Laplace transformation → £-1{F(s)}=f(t), to return to time domain

During calculations of Laplace transformations of various functions, formulas for Laplace transformations of basic functions are applied. It is possible to calculate transformation for functions, which are considered in examples, but the easiest way is application of formulas for basic transformations. During calculations differential equation transformed to Laplace form is smashed to simple fractions. In the next step simple fractions are compared with formulas for Laplace transformations of basic functions.
Laplace transformations of basic functions - formulas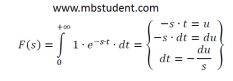
Function f(t), in domain of time, is described by equation → f(t)=1(t). Laplace transformation will be calculated for considered function. Note a fact that 1(t)=t0. Laplace transformation of function f(t) → F(s) will be calculated with application of theorem about integration by substitution.
Laplace transformation - solved example 1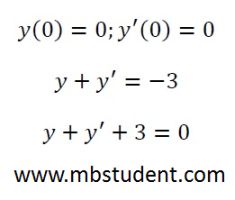
Laplace transformation will be applied to calculate differential equation of the second row → y'+y=-3. Differential equation has initial conditions y(0)=0, and y'(0)=0. Laplace transformation form Y(s) of function y(t) will be calculated. Function in form Y(s) will be smashed to simple fractions. In the last step inverse transformation on function Y(s) will be executed to find function y(t), which is in domain of time. During execution of inverse Laplace transformation, formulas for Laplace transformations of basic function will be applied.
Laplace transformation - solved example 2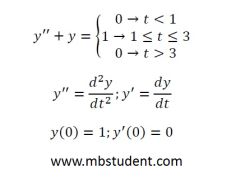
Solved example with Laplace transformation applied to solve differential equation.
Laplace transformation - example 0
Solved example with Laplace transformation applied to solve differential equation.
Laplace transformation - example 1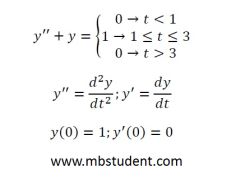
Solved example with Laplace transformation applied to solve differential equation.
Laplace transformation - example 2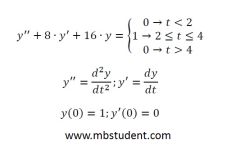
Solved example with Laplace transformation applied to solve differential equation.
Laplace transformation - example 3