


Collection of examples with solutions indefinite integrals. Functions integration is inverse operation in comparison to functions derivatives calculation. In general integration is a summing of elementary elements dx.

Set of formulas for indefinite integrals of elementary functions.
Indefinite integrals of elementary functions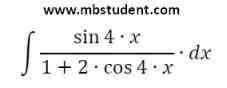
Solved example with indefinite integral of function f(x)=sin(4·x)/(1+2·cos(4·x)).
Indefinite integral - example 1
Solved example with indefinite integral of function f(x)=(3·x+7)1/2.
Indefinite integral - example 2
Solved example with indefinite integral of function f(x)=2/(3·x+1).
Indefinite integral - example 3
Solved example with indefinite integral of function f(x)=(1+sinx)1/2·cosx.
Indefinite integral - example 4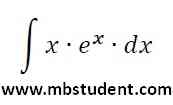
Solved example with indefinite integral of function f(x)=x·ex. Theorem about integration by parts is used.
Indefinite integral - example 5
Solved example with indefinite integral of function f(x)=x3·ln(x). Theorem about integration by parts is used.
Indefinite integral - example 6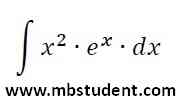
Solved example with indefinite integral of function f(x)=x2·ex. In example theorem about integration by parts is used twice. At the end of integration, a derivative of integrated function is calculated in purpose to check integration correctness.
Indefinite integral - example 7
Solved example with indefinite integral of function f(x)=x3·ex2. In example theorem about integration by parts is used three times. At the end of integration, a derivative of integrated function is calculated in purpose to check integration correctness.
Indefinite integral - example 8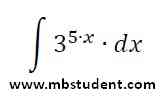
Solved example with indefinite integral of function f(x)=35·x. In example theorem about integration by substitution is applied. At the end of integration, a derivative of integrated function is calculated in purpose to check integration correctness.
Indefinite integral - example 9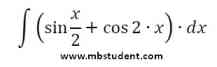
Solved example with indefinite integral of function f(x)=sin(x/2)+cos(2·x). In example theorem about integration a sum of two functions is applied.
Indefinite integral - example 10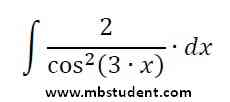
Solved example with indefinite integral of function f(x)=2/(cos2(3·x)). In example theorem about integration by substitution is applied.
Indefinite integral - example 11
Solved example with indefinite integral of function f(x)=1/(1-sin2(x)). Pythagorean identity is applied during calculations. Application of Pythagorean identity allows to recalculate function to form of elementary function.
Indefinite integral - example 12
Solved example with indefinite integral of function f(x)=(1-sin2(x))/cos(x). Pythagorean identity is applied during calculations. Application of Pythagorean identity allows to recalculate function to form of elementary function. Pythagorean identity → sin2x + cos2x = 1.
Indefinite integral - example 13
Solved example with indefinite integral of function f(x)=(1-cos2(x))/sin(x). Pythagorean identity is applied during calculations. Application of Pythagorean identity allows to recalculate function to form of elementary function. Pythagorean identity → sin2x + cos2x = 1.
Indefinite integral - example 14
Solved example with indefinite integral of function f(x)=1/(x2+8). In example theorem about integration by substitution is applied. Formulas for integrals of elementary functions are also used.
Indefinite integral - example 15