Node voltage method is one of methods used for electrical network analysis. Node voltage method is based on Kirchhoff’s current law. We can say that node voltage method does not see physical voltage sources. In node voltage method we have to transform all voltage sources to virtual current sources. Additional important rule of node voltage method is that we have to assume that one of node has electric potential equal to zero. On schematics we mark it by connecting symbol of ground to chosen node.
Derivation of node voltage method
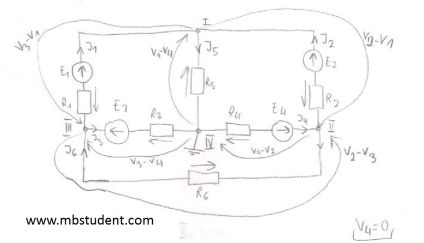
Node voltage method is based on Kirchhoff’s laws for electrical circuits. In this example, Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL) equations will be written. In the next step these equations will be transformed to create node voltage method equations. Node voltage method has advantage over branch current method because number of equations to calculate is smaller.
Derivation of node voltage method
Node voltage method example 1
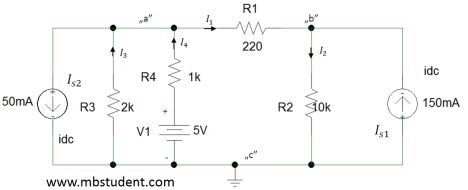
Application of node voltage method for electrical circuit which is built with two current sources and one voltage sources. Circuit has also four resistors in its topology. In solution voltage source will be transformed to virtual current source.
Node voltage method – example 1
Node voltage method example 2

Application of node voltage method for AC circuit which is built with one current source and one voltage source. Circuit has also resistor R, capacitor C and inductivity L in its topology.
Node voltage method – example 2
Node voltage method example 3
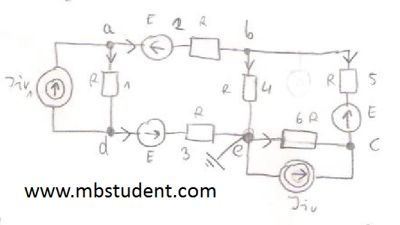
Application of node voltage method for electrical circuit which is built with two current sources and one voltage sources. Circuit has also four resistors in its topology.
Node voltage method – example 3
Node voltage method example 4
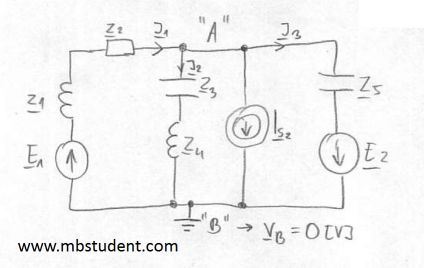
Electrical circuit contains two sinusoidal voltage sources and one sinusoidal current source. Circuit has in its topology also passive parts like resistor, inductivity and capacitors. Node voltage method will be used to calculate branch currents.
Node voltage method – example 4
Node voltage method example 5
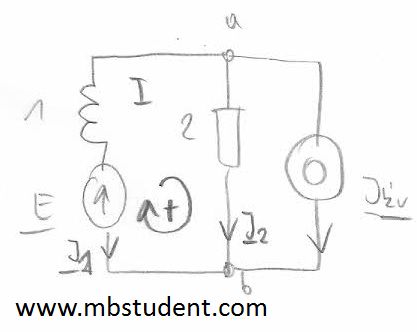
Application of node voltage method for AC circuit. Electrical circuit is built from: voltage source, current source, inductivity and resistor. In example solved below is also comparison of node voltage method with mesh current method.