Solved examples from mechanics statics. Statics, which is a field of mechanics, treats about influences between bodies which do not move. In brief, it is proper to say that motion in statics does not exist. Equilibrium equations are often designated in statics. In general case six conditions have to be met for body to stay at rest. We have to assign to our issue coordinate system. The most popular coordinates system is Cartesian coordinates system XYZ which has three dimensions. As it was said earlier, six conditions have to met:
⋅ Sum of forces which works along X axis has to be equal to zero: ΣFix=0
⋅ Sum of forces which works along Y axis has to be equal to zero: ΣFiy=0
⋅ Sum of forces which works along Z axis has to be equal to zero: ΣFiz=0
⋅ Sum of torques which works around X axis has to be equal to zero: ΣTix=0
⋅ Sum of torques which works around Y axis has to be equal to zero: ΣTiy=0
⋅ Sum of torques which works around Z axis has to be equal to zero: ΣTiz=0
Equilibrium of frame under continuous load – example 1
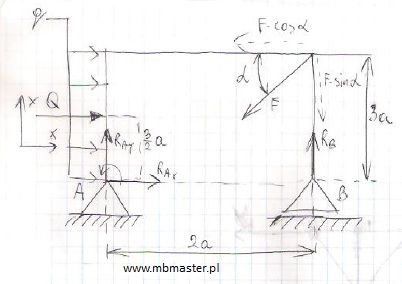
Equilibrium equations designation for frame under continuous load q[N/m]. Frame has shape like sign [ which was rotated by π/2 to right side. Frame stands on unmovable support on the left. Frame stands on moveable support on the right. Considered example is two dimensional.
static equilibrium equations example 1
Equilibrium equations – example 2
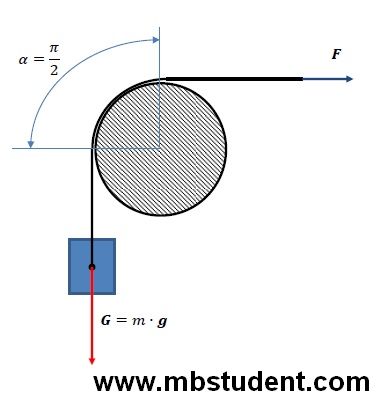
Cable is rolled around unmovable roller. We assume that cable is massless. Weight with mass m[kg] is hanged at the one of cable ends. Sliding friction exists between roller’s surface and cable. Sliding friction is described and sliding friction factor μ[-]. Cable is rolled around roller on the one quarter of its circuit. Roller cross-section is a wheel. Force F has to designated. Force F is responsible for keeping system in equilibrium.
static equilibrium equations example 2
Equilibrium equations- example 3

Beam is hanged to ceiling via two ropes. Ropes are massless. Beam has mass m[kg]. Force F[N] works in specified beam’s point. In example equilibrium equations for system have to calculated. Reaction forces in ropes also have to be calculated. Beam is under gravity field. Beam has length 8·a. Gravity force which works on beam has to be placed in beam’s gravity center C.
static equilibrium equations example 3
Sliding friction example 1
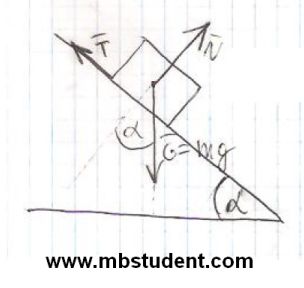
Material point with mass m is on the slope. Slope is inclined by angle α. Between slope surface and material point exists static sliding friction described by factor μ. Subject of example is to find angle αmax in equilibrium position.
Rolling friction example
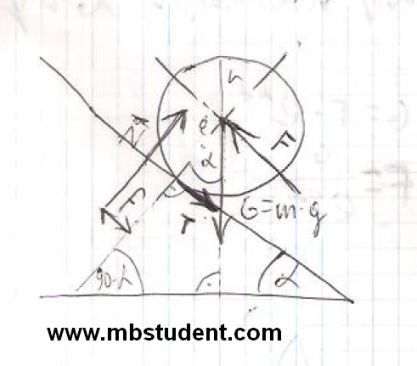
Roll is on the silppery slope. There is rolling friction between slope’s surface and roll. Sliding friction also exists between roll and slope’s surface. Subject of example is to designate equilibrium equations. Next we have to calculate vaule of force F which keeps roll in rest. Force F doesn’t let roll down the slope. Slope is inclined by angle α.