Designation of stress in various systems of beams in which shear force and bending torque are calculated analytically. Static equilibrium equations are written for every analyzed example.
This page contains set of solved examples from mechanics of materials. On this it’s possible to find various examples in which stress in beams is designated. Examples which are placed here you can learn following:
• designation of equilibrium equations
• calculation of shear force
• designation of bending torque
• designation of torsion torque
• designation of maximum stress
Designation of stress in the beam – example 1
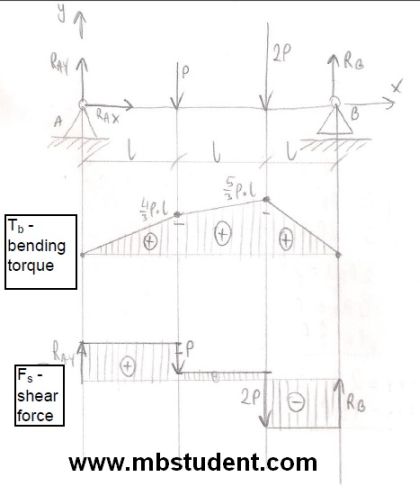
Beam stands on two supports. First support is unmovable. Second support can move in one direction. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam.
Stress in the beam – example 1
Designation of stress in the beam – example 2
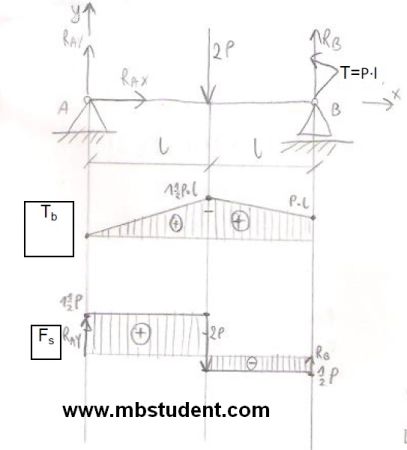
Beam stands on two supports. First support is unmovable. Second support can move in one direction. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam.
Stress in the beam – example 2
Designation of stress in the beam – example 3

Beam stands on two supports. First support is unmovable. Second support can move in one direction. Continuous load q[N/m] works on beam. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam.
Stress in the beam – example 3
Designation of stress in the beam – example 4
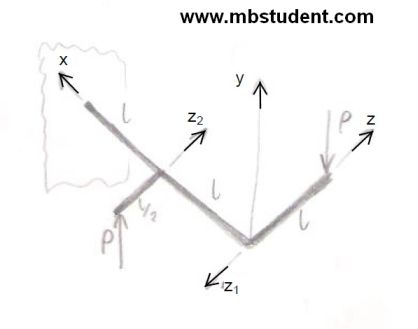
Beam is fixed to the wall. Three dimensions coordinates systems is assigned to beam. On beam work forces, bending torques Tb and torsion torques Tt. In example we will designate reduced vicarious torque and reduced vicarious stress.
Stress in the beam – example 4
Designation of stress in the beam – example 5
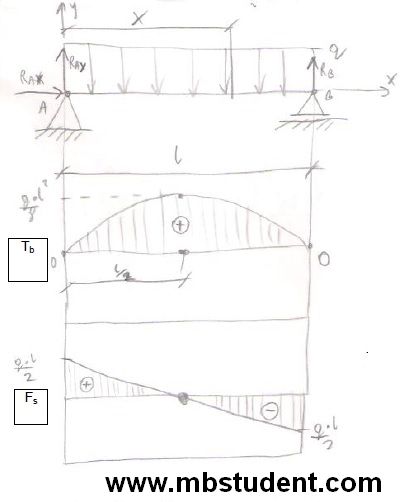
Beam stands on two supports. First support is unmovable. Second support can move in one direction. Continuous load q[N/m] works on beam. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam. Maximum stress is calculated. Beam has specific section shape. Moment of inertia for section it’s designated.
Stress in the beam – example 5
Designation of stress in the beam – example 6

Beam stands on two supports. First support is unmovable. Second support can move in one direction. Two external forces work on beam. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam. Equilibrium equations also will be designated.
Stress in the beam – example 6
Designation of stress in the beam – example 7
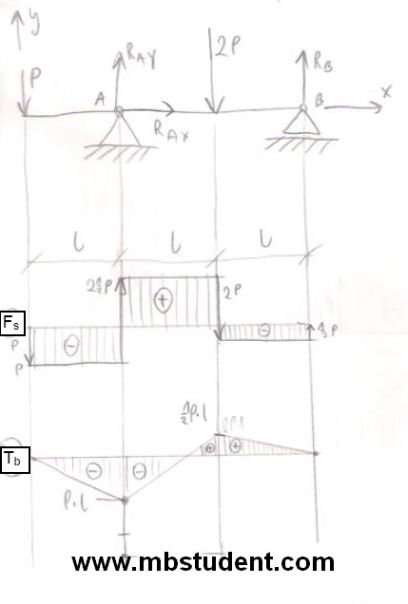
Beam stands on two supports. First support is unmovable. Second support can move in one direction. Two external forces work on beam. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam. Equilibrium equations also will be designated.
Stress in the beam – example 7
Designation of stress in the beam – example 8

Beam stands on two supports. First support is unmovable. Second support can move in one direction. Continuous load q[N/m] works on beam. In example we will designate characteristics of shear force Fs and bending torque Tb at whole length of beam. Equilibrium equations also will be designated. Maximum bending torque as a function of length is calculated.
Stress in the beam – example 8
Designation of stress in the beam – example 9
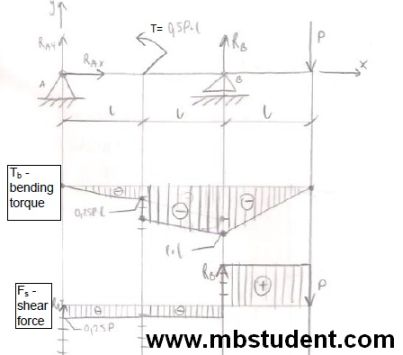
Beam stands on two supports. First support is unmovable. Second support can move in one direction. External force P and external bending torque work on beam. Characteristics of shear force Fs and bending torque Tb will be calculated at whole length of beam. Equilibrium equations also will be designated. Maximum bending torque as a function of length is calculated.
Designation of stress in the beam – example 9
Designation of stress in the beam – example 10
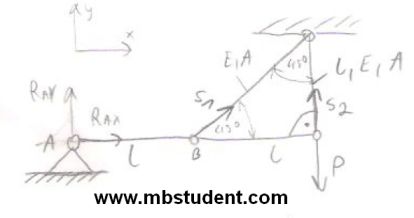
Beam stands on one support. Support is unmovable. Beam is also fixed to the ceiling by two rods. Rods are fixed to the beam in its specific points. External force P works at the end of beam. Hooke’s law will be applied to calculate stress in the beam. Equilibrium equations for forces and torques will be written. Minimum beam’s cross-sectional area A has to calculated to provide enough strength for beam.
Stress in the beam – example 10
Designation of stress in the beam – example 11
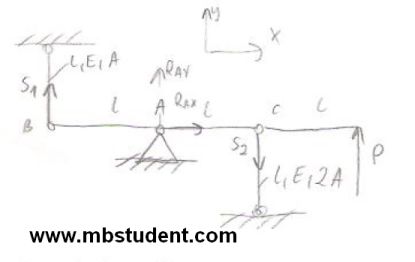
Beam stands on one support. Support is unmovable and it’s placed directly in its middle. Beam is fixed to the ceiling and to the ground by rod. Rods are fixed to the beam in its specific points. External force P works at the end of beam. Hooke’s law will be applied to calculate stress in the beam. Equilibrium equations for forces and torques will be written. Minimum beam’s cross-sectional area A has to calculated to provide enough strength for beam.
Stress in the beam – example 11
Designation of stress in the beam – example 12
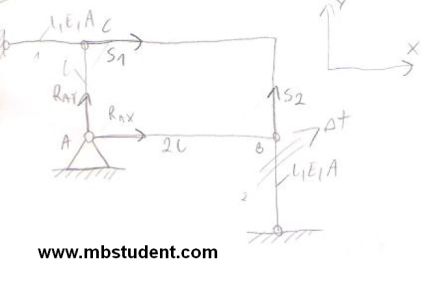
Frame is built with four steel rods. Frames shape is a square. In one point frame is connected to the ground by unmovable support. Frame is also connected to two additional unmovable supports by rods. In specific time on one of frame’ side works higher temperature. As a result of higher temperature one of frame’s rods had extended its length and thermal stresses appeared. Hooke’s law will be applied to find reaction forces in frame. Frame’s dimensions are known.