In forward kinematics, robot’s joint angles and joint shifts values are known. Robot may have various types of drives in its construction. Drives can be rotary drives or linear drives, it depends of robot’s destination. In forward kinematics it is possible to calculate position of an item from various Cartesian coordinates system to various Cartesian coordinates system which are assigned to robot’s joints. We most calculate the most positions from tool’s coordinates (it is the last coordinates system assigned to robot construction) to base coordinate system (sometimes called zero coordinates system). Base coordinates system is always unmovable. In forward kinematics we use Denavit-Hartenberg notation. Denavit-Hartenberg parameters are written into table. Next step is creating transformation matrix. Forward kinematics could be symbolically marked in short relation:
{Θi, di} → {Xi, Yi, Zi}
Denavit-Hartenberg parameters are used during designation of transformation matrix. Transformation matrix defines transformation from coordinates system “i” to coordinates system “i-1”.

Forward kinematics – example 1
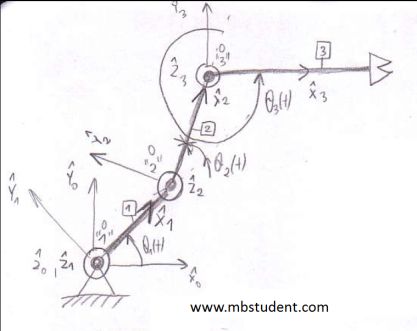
Forward kinematics of RRR manipulator. RRR manipulator is a model of robot which contains three rotary joints. In first step coordinates systems are assigned to manipulator joints. Assigning of coordinates systems is made via Denavit-Hartenberg notation. At second step table with Denavit-Hartenberg’s parameters is written. Robot has three joints then number of coordinates systems is equal to three. General form of transformation matrix is used. Transformation matrices between consecutive coordinates systems are written. As a result three transformation matrices are obtained. Transformation matrix which describes any position from last coordinates system in base coordinates system, is obtained by multiplying transformation matrices between consecutive coordinates systems.
Forward kinematics for robot – example 1
Forward kinematics – example 2
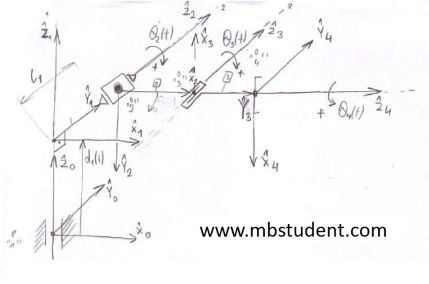
Robot has one prismatic joint and three rotary joints in its construction. Table with Denavit-Hartenberg parameters is written for robot. Because robot has four joint, four transformation matrix are obtained. Each transformation matrix is for two consecutive coordinates systems. To write transformation matrix between coordinate system a general form of transformation matrix is used. Transformation matrix which describes any position from last coordinates system in base coordinates system, is obtained by multiplying transformation matrices between consecutive coordinates systems.
Forward kinematics for robot – example 2
Forward kinematics – example 3
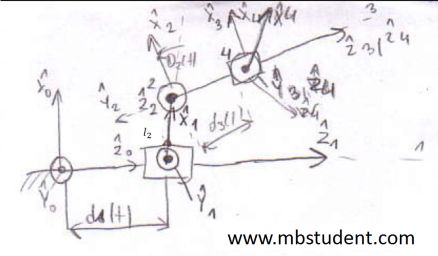
Robot has two prismatic joints and two rotary joints in its construction. Table with Denavit-Hartenberg parameters is written for robot. Because robot has four joint, four transformation matrix are obtained. Each transformation matrix is for two consecutive coordinates systems. To write transformation matrix between coordinate system a general form of transformation matrix is used. Transformation matrix which describes any position from last coordinates system in base coordinates system, is obtained by multiplying transformation matrices between consecutive coordinates systems.
Forward kinematics for robot – example 3
Forward kinematics – example 4
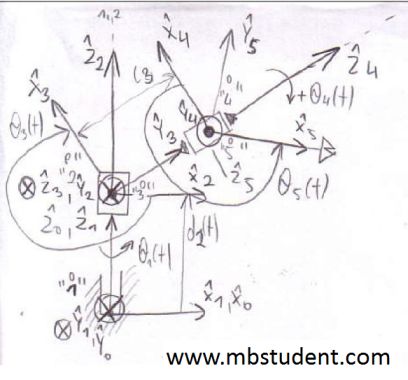
Considered model of robot has four rotary joints and one prismatic joint. Coordinates systems are assigned to robot’s construction via Denavit-Hartenberg notation. Because robot has five joints as a result five coordinates systems are obtained. Between two consecutive coordinates systems transformation matrix is designated. Robot has five joints so five transformation matrices are obtained. Transformation matrix which describes any position from last coordinates system in base coordinates system, is obtained by multiplying transformation matrices between consecutive coordinates systems.