One of basic interests of control theory is to examine how looks system behavior for various input signals or extortions. Input and output signals are always in domain of time, however, to obtain transfer function signals magnitudes have to transformed from time domain to complex variable s domain. To do that Laplace transformation is applied. On this website a few examples about calculating system response are placed. It is very comfortable to describe automation object in one equation. For some objects it is possible to describe them with transfer function H(s). If transfer function H(s) is known then it is tied in one equation with Laplace transformations of input and output signals → Y(s)=H(s)·X(s).
Automation object response – example 1

Output signal in certain automation object is described by differential equation 2·x”+3·x’+x=4. Output signal function has start conditions x(0)=1 and x'(0)=1. Differential equation which describes output signal will be solved with Laplace transform. After transformation output signal to Laplace from, it was smashed to simple fractions. Originals of simple fractions transformations will be designated. Heaviside’s formulas will be used to calculate factors of simple fractions originals.
automation object response – example 1
Automation object response – example 2
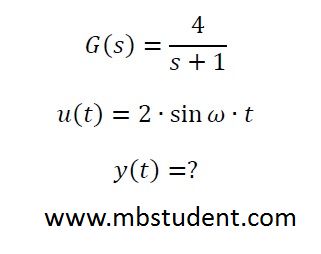
Mathematical model of object is described by transfer function H(s)=4·(s+1). On object’s input is a signal u(t)=2·sin(ω·t). Purpose of example is to designate output signal y(t). Designate Laplace transformation of output signal Y(s)=H(s)·U(s). Laplace transformations and its originals will be designated with formulas for Laplace transformations of basic functions.
automation object response – example 2
Automation object response – example 3
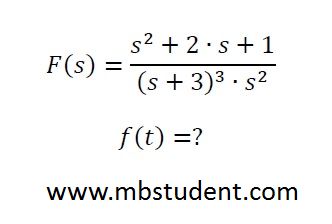
Laplace transformation of object’s disruption signal is known. Disruption signal is described by operator equation F(s)=(s2+2·s+1)/((s+3)3·s2). Original of disruption signal’s Laplace transformation has to be found. Original of Laplace transformation is in time domain. Formulas for basic Laplace transformations are being used. Heviside’s formulas will be used to calculate factors of original function.
automation object response – example 3
Automation object response – example 4

Laplace transformation of object’s disruption signal is known. Disruption signal is described by operator equation F(s)=(s2+1)/(s·(s+1)·(s-2)). Original of disruption signal’s Laplace transformation has to be found. Original of Laplace transformation is in time domain. Formulas for basic Laplace transformations are being used. Heaviside’s formulas will be used to calculate factors of original function.