Application of branch current method for calculation of currents and voltages in electrical circuits. Electrical DC circuits and electrical AC circuits considered. Branch current method is based on Kirchhoff’s current law (KCL) and Kirchhoff’s voltage law (KVL).
Kirchhoff’s current law (KCL) tells us that the algebraic sum of currents which flow to and flow out from node is equal to zero. Kirchhoff’s current law came from the principle of electric charge conservation. When we apply Kirchhoff’s current law we use convention that currents which flow in direction to node are with sign “+” and currents which flow in direction out from node are with sign “-“.
Kirchhoff’s voltage law (KVL) tells us that the algebraic sum of voltages in specified mesh is equal to zero. Kirchhoff’s voltage law came from the principle of energy conservation. Application of Kirchhoff’s volatge law is folowing. In specified mesh we mark a direction of voltages circulation. When voltages in mesh has equal direction we give them sign “+” otherwise we give them sign “-“.
Procedure of branch current method is following. In this method we have to write equations for Kirchhoff’s current law and Kirchhoff’s voltage law. Number of equations for each law is specified and it’s given by following formulas:
Number of equations for Kirchhoff’s current law is equal to number of nodes minus one. Symbolical we write it:
KCL → (n-1)
where:
n – number of nodes
Number of equations for Kirchhoff’s voltage law is equal to number of branches in circuit minus number of equations for Kirchhoff’s current law. Remember that current source is not a branch. Symbolical we write it:
KVL → m-(n-1)
where
m – number of branches
n – number of nodes
Branch current method example 1
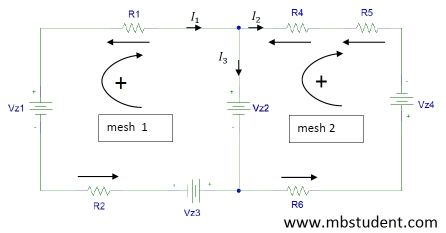
Application of branch current method for electric circuit which is built from four voltage sources and five resistors.
Branch current method – example 1
Branch current method example 2

Application of branch current method for electric circuit which is built from two current sources, three voltage sources and four resistors.
Branch current method – example 2
Branch current method example 3

Application of branch current method for electric circuit which is built from two current sources, three voltage sources and five resistors.
Branch current method – example 3
Branch current method example 4

Electrical circuit represents a model of one phase from three phase AC motor. Model of inductive motor’s phase is often used for theoretical calculation of currents. In this exercise branch current method will be used to find expressions for currents in AC motor’s model.
Branch current method – example 4
Branch current method example 5

Branch current method will be applied to calculate branch currents in electrical AC circuit. Electric circuit is built with alternate voltage source E, alternate current source I. Electric circuit has also passive elements in its topology. Circuit contains three impedances which came from following elements: inductivity L1, capacitor C1 and resistor R1. Branch currents are calculated in example with application of complex numbers.
Branch current method – example 5
Branch current method example 6

Branch currents will be calculated in electrical AC circuit. Electric circuit contains in its topology one alternate voltage source Vs and one alternate current source Is. Because it is an AC circuit all calculations are made using complex numbers. Circuit is built with five impedances which are tied with passive elements like inductivities L1 and L2, resistors R1 and R2 and one capacitor C1.
Branch current method – example 6
Branch current method example 7

Branch currents will be calculated for DC electrical circuit. Electric circuits contains in its topology voltage source, two resistors, one inductivity and one capacitor. We apply branch current method for electric circuits in stable state(non-transient). For electrical DC current, we treat ideal inductivities and ideal capacitors in special way. Ideal inductivity is a short circuit for DC current. Ideal capacitor is a break for DC current.
Branch current method – example 7
Branch current method example 8

Branch currents will be calculated for DC electrical circuit. Electrical circuit is built with two voltage sources and five resistors. Circuit has two meshes in its topology. Voltage sources are connected in circuit in different ways, so you should take this fact under consideration during writing Kirchhoff’s equations. Total resistance of circuit will be calculated in purpose to find a value of circuit’s main current.