Control theory is a field of knowledge which examines methods which allow to control specific objects. Control therory draws from other field of knowledge like maths, physics, electrical engineering and mechanical engineering. Maths is widely applied in control theory since it allows to create objects models which could be later implemented into controllers. Need of proper control growth in science years ago, people are lazy and thier laziness is a key of our progress. The result of this progress is control theory.
System responses for various extortions:
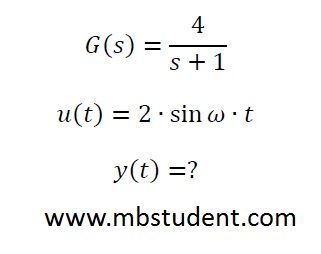
In control theory we examine how looks system behaviour for various input signals or extortions. Input and output signals are always in domain of time, but to obtain transfer function we transfer magnitudes which are function of time to magnitudes which are functions of complex variable s. To do that we use Laplace transformation. On this website a few examples about calculating system response are placed. It is very comfortable to describe automation object in one equation. For some objects it is possible to describe them with transfer function H(s). If transfer function H(s) is known then it is tied in one equation with Laplace transformations of input and output signals → Y(s)=H(s)·X(s).
Laplace transformations of various system responses
Transfer functions examples:

Set of examples in which transfer function is designated for various mechanical systems and electrical circuits. All calculations are made using Laplace transformation. Transfer function is one of methods for creating dynamic model of system. In short definition we can define transfer function as a Laplace transformation of output signal Y(s) divided by Laplace transformation of input signal X(s). Dynamic model of object in transfer function form H(s) is very comfortable because it links in one equation relation between input and output signal.
Transfer functions for various systems
State space representation examples:
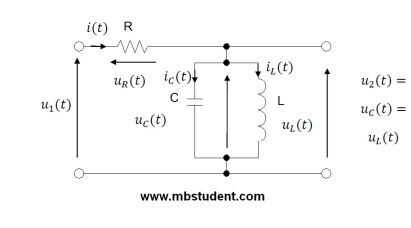
State space representation uses state variables for object description. Every state variable is tied with “energy warehouse”. Mechanical and electrical objects have a few types of “energy warehouses”.
Energy warehouses for electrical systems are:
• capacitor C → capacitor stores energy in electric field
• inductivity L → inductivity stores energy in magnetic field
Energy warehouses for mechanical systems are:
• mass m → stores kinetic energy during progressive movement
• inertia I → stores kinetic energy during rotary movement
• mass m → stores potential energy in gravity field
General form of state space representation equations:


On this website are placed solved examples in which state space representation and transfer functions are designated for various system. Designating two kinds of dynamic models allows to compare them. Examples placed here contain also sample codes for using with MATLAB. Using mentioned sample codes it is possible to simulate system behavior and plot various characteristic like step response, impluse response and frequency plots.
Designating dynamic models as state space representation equations for various electrical system. Beside state space representation, transfer function is also calculated. It is possible to compare both models. As an annex you can find here sample codes to use in MATLAB which allow you to plot impulse response, step response and frequency characteristics.