Mathematics is the tool and the language of science. Without very good skills in maths it is highly impossible to understand practically every strict subject, thus, it determines how it is important. It is true to say that with maths everything but without maths nothing. I advise you to exercise math because it will pay off in future and these are not only empty words but pure true. Plenty of examples from higher mathematics are solved here. Every example is solved step by step, therefore, it will easy to understand what author thought during computation.
Derivatives of functions

Collection of solved examples about calculation of function derivatives. Various of derivatives are calculated in this set. Calculation of function derivative is the first step to examine how function behaves, therefore, strong abilities in this field of higher maths are necessary in order to understand more advanced subjects. Various function derivatives are calculated in this set of examples. There are computed derivatives of:
• multiplies of functions
• complex functions
• trigonometric functions
Functions derivatives examples
Indefinite integral examples
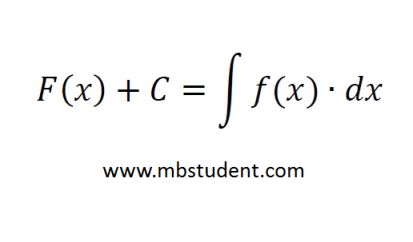
Set of solved examples with indefinite integrals. Calculation of indefinite integral is an inverse operation to calculation of function derivative.
Definite integral examples

Set of solved examples with definite integrals. Definite integrals are widely applied in practice because as a result of definite integral a numeric value is obtained. Single definite integral could be interpreted geometrically as a section area under function line. Single definite integral is the most simple form because double definite integrals and triple definite integrals also exist, however, they are applied to calculate more complex issues like specific areas, volumes or inertias.
Differential equations examples
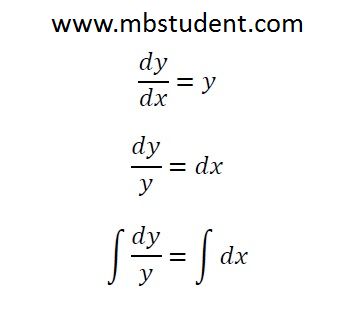
Differential equations are advanced part of higher mathematics. In engineering and strict subjects are really often applied. Plenty of physical phenomenas are described by differential equations. You will find here set of examples which I believe will help you understand this subject.
Differential equations examples
Laplace transformation examples
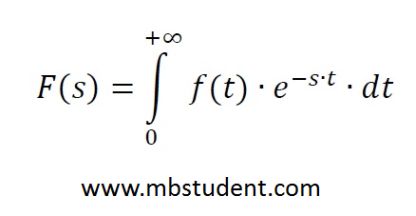
Set of examples with Laplace transformation. Laplace transformation is one of method for solving differential equations. This method is often used in various fields of strict sciences, for example, physics, electrical engineering, and control theory. Procedure for solving differential equation with application of Laplace transformation is following:
• transform equation to Laplace form → £{f(t)}=F(s)
• write expression F(s) on equations left side, the rest on te right side
• smash left side of equation to simple fractions
• calculate factors, by which fractions are multiplied
• compare simple fractions,which are in Laplace transformation form, with formulas for basic Laplace transformation
• execute inverse Laplace transformation → £-1{F(s)}=f(t), to return to time domain