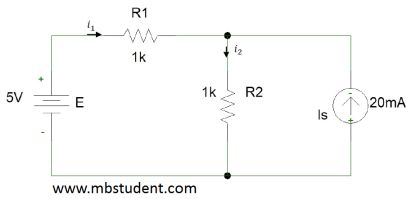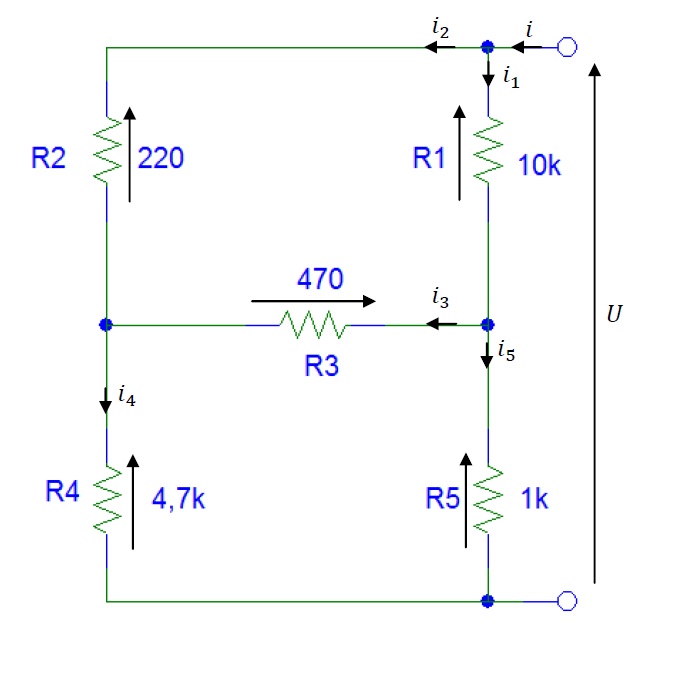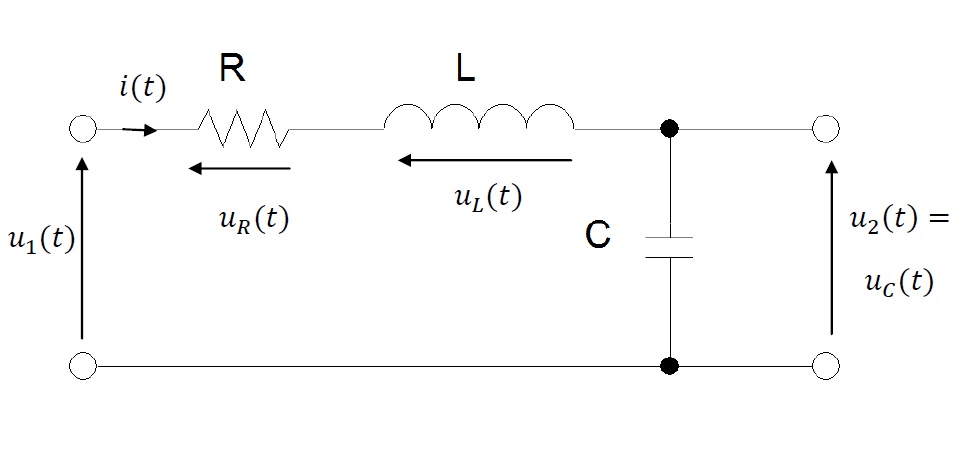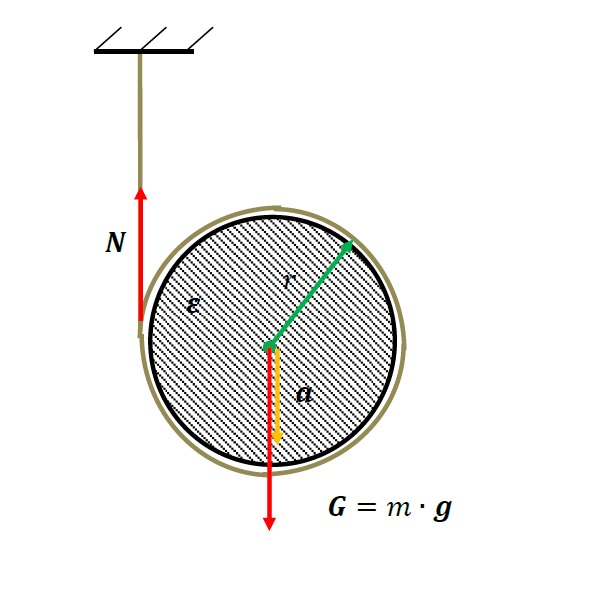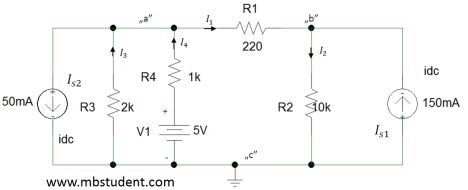
Nodal analysis is one of methods used for electrical networks analysis. Nodal analysis is based on Kirchhoff’s current law. Main idea of this method is to calculate electrical potentials of every node. This will allow to calculate voltages in branches since voltage is a difference of potentials. This approach has one rule which requires to assume that potential of one chosen node has be equal zero volts. Symbolically this chosen node is connected to the ground on electrical diagram.